The Minimization and Conjugation Algorithms

 

The algorithms are based on a discrete model, instead of approximating the continuous case discrete surfaces (i.e. triangulations) are considered and the terms from the continuous case are redefined on the discrete level.

A map between discrete surfaces with the same underlying topological simplicial complex (i.e. triangulations with the same discretization) maps corresponding points onto each other, it is linear on each triangle. The Dirichlet energy of such a map is defined as the sum of the Dirichlet energies of the (smooth) linear maps of the triangles. It turn out that there is an explicit representation of in terms of the angles of the domain triangles and the side lengths of the image triangles:

where are the edges in the image and and are the angles in the domain opposite to the edge corresponding to .

Analogous to the continuous case a discrete harmonic map is defined as a critical point of the Dirichlet energy functional with respect to variations of the interior image vertices, to be able to model free boundary problems boundary points on straight resp. planar symmetry lines are allowed to vary along the image line resp. within the image plane. The condition for f to be a critial point is that for each (interior) image point p

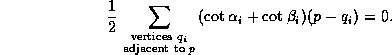
The Dirichlet energy can be written as a quadratic form with a suitable representation P of the image points and a symmetric positive definite sparse matrix S. For computing a discrete harmonic map this quadratic form has to be minimized, two different methods are available:

,

Solve the problem directly by computing an LU decomposition of the matrix S. If this method is used the conjugation algorithm (see below) cannot be applied to the solution because all boundary points are assumed to be fixed. Another drawback is that the full matrix has to be stored therefore this method should only be used for small numbers of points (for larger numbers of points this method is much slower then the CG method anyway).

,

Use a conjugate gradient method for sparse matrices to compute the minimum. This method also handles boundary points on symmetry lines, it must be used to be able to apply the conjugation algorithm.

Both the LU and the CG method can be applied to a single geometry of class Geom2d or one step of a Surface instance using the buttons. The methods can only be used for a Surface instance, in this case the minimization method is applied to all steps. The methods on Surface copy the domain surface (which is needed for the conjugation) to the domain geometry before applying the minimization algorithms.

There is also a version of the Dirichlet minimizer for surfaces in spherical and hyperbolic space (the methods) but it's quite difficult to use it because the metrics and projections (especially in the hyperbolic case) have to be handled.

To compute a discrete minimal surface the computation of discrete harmonic maps has to be iterated. Starting with an initial surface (i = 0) the surface is computed from the given surface as the minimum of where X has the same discretization and boundary restrictions as . It can be shown that if no triangles degenerate (a subsequence of) the surfaces converges uniformly to a limit surface M, a discrete minimal surface.

The conjugation algorithm is defined for discrete harmonic maps therefore it can not only be applied to the limit surface M but also to all intermediate surfaces -- the minimization algorithm only has to be applied once to be able to compute a conjugate surface. Since the algorithm uses the discrete data from the minimization process directly to compute the discrete conjugate surface it avoids the problem that occur when the smooth case is simulated.

This is how the discrete conjugate surface is computed (please see [PP] on how boundary points are handled and why the result can be called the conjugate surface). The minimality condition geometrically means that for each point p the weighted edges emanating from p add up to zero, therefore they can be arranged to a closed polygon, the dual cell of p. The dual cells can be assembled to a well defined dual graph and the centers of the cells give the discrete conjugate surface which has the same discretization as the surfaces (both the dual cells and the conjugate surface are drawn while they are computed).

The algorithm can be applied to the current step/all steps of a Surface instance with / , the result is stored in the conjugate geometry which can be viewed by setting the display method to "conjugate-disp" or switching the task to (see 8.2.3.1). The LU minimization can only be used to compute the discrete harmonic map if all boundary points are fixed, if there are boundary points on symmetry lines the CG minimization algorithm has to be used to be a able to conjugate the surface.