The Concept of Moving and Tracing

 

In the introductional section we have described the application of static visualization techniques on time cuts of dynamical processes. But these visualization techniques on time cuts are not the only possible approaches to get a deeper insight into the behaviour of interesting phenomena in time. A different approach examines integrated evaluations on the process. They are also of great importance in numerical approaches based on the method of characteristics. Let us think for example of a flow problem, where a vector field v describes the movement of particles or sets of the latter in time. In detail this means that a particle x at time in a domain g moves according to the first order differential equation with the initial condition . The stationary visualization methods allow us to inspect this field at certain times from the point of view of a fixed observer, where we can interactively vary time and method parameters in the way it is described in other sections. In comparison to that the integration techniques let us have a closer look on the evolution itself. This means we follow sets of particles in time and record there behaviour in some sense in terms of a moving observer. In the framework of continuum mechanics these two different visualization approaches reflected the two main different coordinate systems, the Lagrangian and the Eulerian coordinates. Now using the integration technique we have two possibilities at hand. The first and standard one is to record only the trace of a set of particles and throw away the time information. The second gives us a complete overview on the movement of the specific set of particles in time. Therefore we extract the movement again as a dynamical process. This new dynamical process then contains the positions and the corresponding times of one particles or of a set of particles, a curve or a surface. We can look at this as a subset of the information of the initial process in which we have performed the integration. Although these two approaches look different from the rendering point of view they can be condensed in one calculation operation.

 
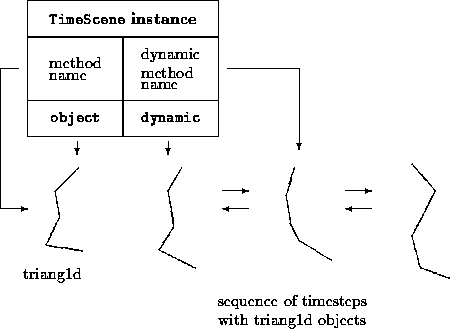
Figure 7.1:  example of tracing

Let us call it moving. Moving always produces a time dependent process move containing the evolution (the movement) of the specific set in space we are interested in. This process is again an instance of class TimeScene. Visualizing this as a trace or as time cuts of the move is then a question of the "display" method on the new process and not of the calculation. In details this means we always calculate moves and then we render them in two different ways. Up to now we only know display methods working on Scene or TimeScene objects, this means on time cuts of the evolution process move. Regarding the possibility to define a "display" method named dynamic_method_name working on the instance variable dynamic, as it is mentioned in the previous section in the description on TimeScene, allows us to display the trace of the process move. We will call this kind of rendering tracing.

To be more explicit let us briefly examine the underlying equation. If is the set to be moved in the field v defined on we want to calculate a one parameter family of sets S(t) which is defined as follows

If S(t) consists of only one point we discretize the differential equation in time. What is actually used is a variant of the second order Euler Cauchy scheme. With the general well known Euler Cauchy scheme we mean the following second order one step ODE method. Its local consistency is of order .

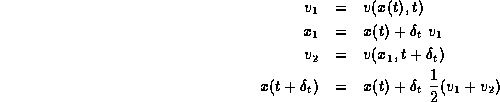
We will use the for the small timestep width in the ODE scheme. Further on we will not store all these timestep but only a few of them. This is possible because of the interpolation techniques working on this list of steps. We will call this larger step width but underlining that it does not depend on the timestep of the process in which we move. The main disadvantage of this standard ODE scheme working on mesh data is that it ignores the special structure of the mesh. The scheme above for example has a consistency error of if the data is smooth. But the vectorfield which is in our case the data is in general not smooth. For viscous flow problems attacked by conforming Finite Element strategies it is only at the edges or boundary surfaces of the elements and for highly inviscous flow numerics and non-conforming Finite Elements it is even worse. We find smoothness only in the interior of the elements. This shows that the standard ODE solves are useless for general situations on discrete meshes. A typical example for the failure of this straightforward approach is the calculation of particle traces passing a shock with a shift in the velocity where according to an adaptation strategy the shock area is intensively refined. The modified scheme we use overcomes this problem. It has a local consistency order of

where h is a local upper bound of the discretizations in space. Fore details we refer to a forthcoming paper.
Now we should turn to the general case were S(t) is no longer a single point. We discretize in space the set S by a triangulated approximation were is a bound for the size of the simplices. Each vertex point of this set will then be moved according to the ODE scheme mentioned above. This defines sets which should approximate . The initial approximation error of with respect to a smooth set S is of the order . But without any mesh adaptation on the meshes we can in general not suppose to be a good approximation of S(t). Therefore we apply an adaptive strategy to refine the discretizations at each timestep following the lines of the adaptive algorithm described in section about dynamical processes and starting with .

Here OneStep is one iteration of the described ODE scheme on the vertex points based on the modified EulerCauchy scheme.

Here the AdaptMesh has to keep aware of degenerating angles as well as of enlarging elements. Let us finally resume that the time scales of the original process and of an arbitrary extracted move process are totally independent.

 
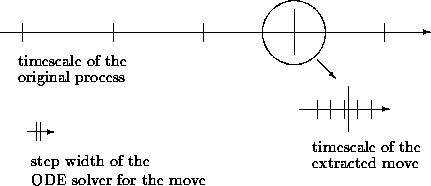
Figure 7.2:  the different scales