
Project D4: 4D structural analysis of the sugar beet geometry
Our goal is developing techniques for model-based 3D reconstruction and classification of storage root geometry from tomographic data, i.e. data obtained from laser scans and MRI. We aim in comparing different cultivars subject to different soil, management and environmental conditions. Furthermore we investigate the temporal variation of sugar beet growth by applying and generalizing regression methods to the space of beets. Our tools are robust and non-supervised, that means they improve previous and-measured methods and corresponding empirical scales. Furthermore, recent results suggest that our methods are capable to statistically separate genotypic from environmental features. Hence the proposed techniques are relevant and effective tools to optimize plant breeding.
Project A6: Mathematical modeling and simulation of microstructured magnetic-shape-memory materials
The macroscopic behavior of magnetic shape-memory (MSM) materials is largely determined by the formation of fine-scale structures, both in the elastic and in the magnetic degrees of freedom. Most practically used samples exhibit additional inhomogeneities on the mesoscale, such as for example the grain structure in polycrystals. The interaction of the two types of microstructure is up to now only poorly understood. Focusing on two occurrences of high current experimental relevance we intend to investigate the role of microstructure for the macroscopic material behavior, and to furnish criteria to improve material production. Building upon the static continuum model developed in the first phase, which permits to resolve the magnetic and elastic structure at scales much smaller than the domain size, we plan: 1) to consider the experimentally relevant case of grains larger than the domain size, where the magnetoelastic behavior of a grain is determined by averaging over the domains; 2) to study dynamics and in particular hysteresis by formulating an evolutionary problem which resolves the motion of individual domain boundaries; and 3) to study the dynamics for grains larger than the domain size, with an averaged version of the evolution model. For each issue we shall address the development of a model, the numerical implementation of the obtained models, and the application to the study of MSM-polymer composites and MSM polycrystals.
Multi-Scale Shape Optimization under Uncertainty
Our project deals with stochastic shape optimization for elastic materials where stochasticity enters the problem both via stochastic loading and stochastic geometry. We intend to bring together the analytical treatment of multi-scale problems via homogenization, the reliable numerical solution of PDE problems on complex domains described via level sets or phase field models, and two-stage stochastic programming approaches using different perceptions of risk aversion. Different concepts of stochastic dominance are becoming increasingly attractive in decision making under uncertainty. They allow for flexible risk aversion via comparison with benchmark random variables. Rather than handling risk aversion in the objective this enables risk aversion in the constraints. In our project this is another conceptual transfer of a paradigm from finite dimensional stochastic programming. Dominance constraints single out subsets of nonanticipative shapes which compare favorably to a chosen stochastic benchmark. The new class of stochastic shape optimization problems we plan to investigate arises by optimizing over such feasible sets. In many real world applications of stochastic shape optimization such as clothes design a nonanticipative prototype shape has to adapt to an uncertain realization of an elastic body. This is quantifiable with various risk measures which go beyond expected value minimization. We intend to apply a principal component analysis to reduce the computational complexity. Our implementation is based on a phase field description of the prototype shape. So far we have studied stochastic shape optimization based on a full resolution of the geometry. In this setting topological modification turned out to be crucial which led us to adapting the concept of topological derivatives for stochastic cost functionals. We intend to advance this research in order to include correlation between separate nearby holes. The same correlations will be studied by a two scale method in which they appear on the micro–scale. We will consider rigorous analysis of this approach and develop an efficient numerical method based on boundary elements on a parametric microscopic shape and macroscopic finite elements. Microstructures will consist of a regular lattice of holes with varying size and orientation. Concrete examples are two shells with perforated connecting material and a hard shell filled with porous material such as bones.
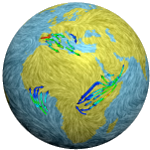
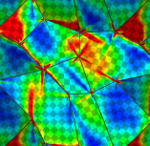
Variational Methods for Model-based Interactive Analysis of Flows
This project aims at an explorative analysis and classification of complex flow pattern such as shear friction, curls or vortices. For real world flows in 2D and 3D and their temporal evolution a fully automatic and global classification is far out of reach. Hence, we will develop a flow exploration method which combines a multi-scale variational approach for the classification of flow pattern with a flexible interface for user guidance. The variational functional consists of a fidelity term, which compares the observed flow locally with parametrized physical or statistically learned models, a prior reflecting the probability of the pattern parameters and its shape, and a suitable functional encoding the user’s guidance and preferences. The analysis tool to be developed will be applied to experimental flow data rendered by different types of image sequences and to flow fields from computational fluid dynamics simulation. The user interactively selects the scale for the flow classification ranging from global macroscopic to local mesoscopic flow phenomena.
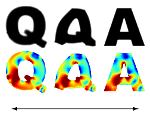
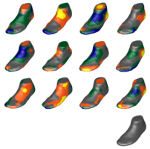
Project C05: Discrete Riemannian calculus on shape space
The theory of shape spaces in vision is linked both to concepts from geometry and from physics. The flow of diffeomorphism approach and the optimal transportation approach are prominent examples for Riemannian metric structures on the space of shapes, intensively studied in the last decade. In general, the numerical realization of the underlying infinite dimensional Riemannian calculus poses enormous computational challenges. In this project we propose suitable time and space discrete approximations. They will be based on optimal matching deformations, which are significantly cheaper to compute but by construction non-Riemannian. We will also study abstract concepts of transportation between metric measure spaces with particular focus on spaces consisting only of a fixed number of points. In the time discrete calculus a discrete path energy is defined as the sum of pairwise deformation energies along a discrete path. Using a variational approach one can deduce from this step by step a discrete logarithm, a discrete exponential map, a discrete parallel transport, a discrete Levi-Civita connection, and finally a discrete Riemannian curvature tensor. This concept will be applied and analyzed in particular for the flow of diffeomorphism and the optimal transportation approach. Furthermore, with respect to a spatially discrete covering of shape space, the approach of deformation based shape dissimilarities will be combined with the diffusion map paradigm expedited by Coifman and coworkers to introduce physically sound and computationally efficient approximations of metric structures on shape spaces. Overall, we aim at combining methods from geometry, stochastic analysis and numerics to advance theory in computer vision and explore new applications with efficient computational tools.

Project C06: Numerical optimization of shape microstructures
This project deals with the two-scale optimization of elastic materials. It is well known that microstructures form when minimizing compliance or tracking type cost functionals, unless a penalty on the area of material interfaces is used. The optimal microstructures are well-understood and can be represented by nested laminates. The laminate construction is an analytically elegant tool but can hardly be reproduced in mechanical devices, nor is it observed in optimization problems posed in nature. Thus, the question arises how close one can get to the optimal design with constructible microstructures. To this end, different approaches will be investigated and compared, namely: microscopic rod models with varying rod thickness, microscopic geometries described by a finite set of parameters, and non-constrained interfaces on the micro-scale with a microscopic interface regularization. To measure the closeness both to the achievable optimal design within the considered class and to a globally optimal laminate design, an a posteriori error analysis will be developed. Here, concepts for a residual error estimation based on the Lagrangian formulation of the optimization problem will be picked up to derive a posteriori estimates for the macroscopic error in the parameters describing microscopic geometries. In addition, the error caused by the chosen microscopic geometric model will be quantified via a posteriori error analysis. These resulting error estimates will be used to implement adaptive algorithms to steer the necessary and sufficient refinement of the macroscopic grid on which the parameters for the microscopic geometries are given and on which the microscopic geometric model is selected. Furthermore, a phase field model will be developed to describe non-constrained material interfaces on the micro-scale, where a diffuse interface energy regularizes the microscopically optimal material design. For this model truly two-scale a posteriori error estimates for the resulting shape optimization problem will be developed. This error analysis will enable mesh adaptivity on both the macro-scale, where the microscopic elastic energy density is evaluated for a given macroscopic elastic displacement, and the micro-scale, where the microscopic energy in dependence of the local microscopic interface geometry is actually computed. Concerning the underlying material design the focus will be on thick elastic domains in 2D or 3D filled with a composite of two different elastic materials or with an elastic and a void phase. As an alternative, rod type models on the micro-scale will be considered. With respect to the physical model, we will mainly deal with linearized elasticity and incorporate nonlinear material laws in later stages of the project. Finally, this project aims at carrying over the two-scale analysis of elastic bulk material to thin elastic shells, where the (in general nonlinear) stored elastic energy of a shell depends on the relative shape operator. Optimization will be performed with respect to the geometry and the thickness of the shell and will later be extended to an optimization of the shell microstructure.

Project 5: Geodesic Paths in Shape Space
This project will provide robust and flexible tools for the quantitative analysis of shapes in the interplay between applied geometry and numerical simulation. Here, shapes S are curved surfaces which physically represent shell-type geometries, boundary geometries of volumetric physical objects, or material interfaces. In isogeometric analysis one faces a wide range of low- and moderate-dimensional descriptions of complicated and realistic geometries. Thus, the geometric description of shapes will be flexible, ranging from simple piecewise triangular to subdivision-generated spline type surface representations and from explicitly meshed volumes to descriptions via level set or characteristic functions. The fundamental tool for a quantitative shape analysis is the computation of a distance between shapes SA and SB as objects in a high- or even 1-dimensional Riemannian shape space. Hence, we aim at developing robust models and fast algorithms to compute geodesic paths in shape space. Both for boundary or interface contours and for shell-type surfaces the Riemannian metric will correspond to physical dissipation either of a viscous fluid filling the object volume or due to a visco-plastic behavior of the shells. The key tool of the proposed approach is a coarse time discretization combined with a variational scheme to minimize the underlying least action functional. For purposes of a geometric analysis not only the resulting value for the distance is of interest. In fact the geodesic paths are natural one parameter families of shapes on which physical simulations and PDE computations can be performed. In case of shapes being represented by shell type surfaces we will apply different approaches: subdivision surfaces generated from coarse surface triangulations and subdivision-based discrete function spaces as a modeling paradigm associated with spline models in CAD, application of methods from discrete exterior calculus on discrete surfaces to derive robust and geometrically consistent discrete shell models, the approximation of curvature-based functionals in shell models via variational principles on general classes of surface meshes. In the case of shapes being boundary contours or material interfaces of volumetric objects we aim at representing shapes via characteristic functions, working in the context of variational methods in BV. We will compare this approach with corresponding models based on level set or parametric descriptions. Here, recent results on global minimization of convex functionals on BV and coarse to fine multi-scale relaxation methodologies will be taken into account. For the numerical discretization we aim at using finite elements.