Recent numerical methods deliver a large amount of data on a lot of different mesh types. The following list shows some of these types.
Finite Element / Finite Volume data is usually given by coefficients to ansatz functions with local support and can easily be evaluated in local coordinates. Therefore a function f on a specific element e of such a mesh can easily be evaluated by a call like f(e,c) where c is the local coordinate vector. For example, for piecewise linear data on triangles, the barycentric coordinates of a point in the triangle are equal to the values of the nodal basis functions. On the other hand, a piecewise polynomial interpolation of Finite Difference data, which are given only at the nodal points of a regular grid, can easily be evaluated using local coordinates as parameters.
As we want to handle `general' elements, we use the following notion of local coordinates that belong to an element: For each element, we specify the dimension of the local coordinate system and the coordinates of all vertices of the element in that local system.
Usually, an n-dimensional element can be parameterized by an n-dimensional local coordinate system, but there are situations where it is more intuitive or appropriate to use a higher dimensional local system. Examples of this are:
As a result, we have to permit local coordinate systems of arbitrary dimension. It is natural to assume that the underlying coordinate space is a standard Euclidian vector space. The following figure shows some examples of possible local coordinate systems for distinct elements. These elements are given as the following range of local coordinates:
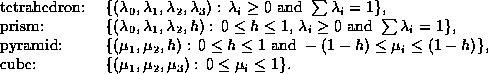
Copyright © by the Sonderforschungsbereich 256 at the Institut für Angewandte Mathematik, Universität Bonn.